Abstract
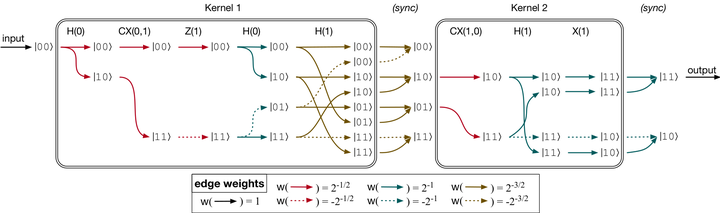
Many circuit simulators use either a Schrödinger-based or Feynman-based approach, which have complementary strengths. Schrödinger-based simulators maintain a state vector by synchronously updating it after each gate (or group of gates), ensuring time efficiency at the cost of exponential space. In contrast, Feynman-based simulators use low space but require high time to compute the sum of exponentially many independent Feynman paths. Because they treat paths as independent, Feynman-based simulators miss opportunities to take advantage of sparsity from destructive interference. In this paper, we present a hybrid Schrödinger-Feynman technique which takes advantage of sparsity by selectively synchronizing Feynman paths. Our hybrid technique partitions the circuit into kernels (groups of gates) and uses Feynman simulation within each kernel. It then synchronizes across the kernels by using Schrödinger-style simulation. We parallelize our approach by representing the simulation as a graph, leveraging state-of-the-art parallel graph algorithms. By selecting kernels carefully, we show that our approach can simulate hundreds of qubits efficiently (in both time and space) on just a single multicore node. In certain “sparse” circuits, we are able to improve running times by multiple orders of magnitude.